Bron: Dit is een van de opgaves van de IOI 2004 in Griekenland

De beroemde beeldhouwer Phidias maakt voorbereidingen voor een nieuw groot kunstwerk. Hiervoor heeft hij rechthoekige marmeren tegels nodig met de afmetingen W1 × H1, W2 × H2, ..., WN × HN. Phidias heeft een groot stuk marmer gekregen, hij wil uit dit grote stuk marmer de tegels van de  gewenste afmetingen zagen.

Er zijn een aantal beperkingen:

• Hij kan een stuk marmer verticaal of horizontaal zagen maar als als hij zaagsnede begint dan moet hij tot het einde doorzagen
• Twee halve tegels kunnen niet aan elkaar gelijmd worden
• Het stuk marmer heeft een patroon dus een tegel met grootte AxB kan niet gebruikt worden voor een tegel grootte BxA, behalve als A=B.

Phidias wil zo min mogelijk van de marmer weggooien.

Voorbeeld:

Het stuk marmer is 21 x 11

En de marmeren tegels die Phidias wil zijn: 10 × 4, 6 × 2, 7 × 5, and 15 × 10.

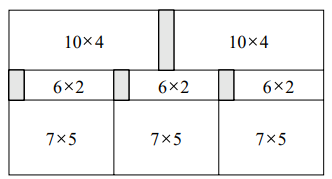
De minimale verspilling is 10, zoals je in het plaatje hierboven kan zien.

 

Invoer

Op de eerste regel staan 2 integer getallen, W, de breedte van het stuk marmer, en H, de hoogte van het stuk marmer. Op de tweede regel staat 1 integer getal N, het aantal tegels. Op de volgende N regels staan de afmetingen van de gewenste tegels, eerst de breedte (Wi), dan de hoogte (Hi) (1 ≤ i ≤ N). Er geldt: 1 ≤ W ≤ 600, 1 ≤ H ≤ 600, 0 < N ≤ 200

 

Uitvoer

De uitvoer bestaat uit 1 integer getal met de minimale verspilling

 

Voorbeeld

Invoer:

21 11

4

10 4

6 2

7 5

15 10

Uitvoer:

10